Die Herleitung der Feinstrukturkonstante

Die Sommerfeldsche Feinstrukturkonstante beschreibt als Kopplungskonstante die Stärke der elektromagnetischen Kraft zwischen zwei Elementarladungen. Die Formel von der Feinstrukturkonstante lautet:

(3‑26)

Mit dem CODATA-Wert 0,00729735253594845000 oder .

Man kann die Feinstrukturkonstante auch mit den quantisierte Größen darstellen. Den ersten Term ersetzen wir mit c² über die Maxwellsche Formel:

Mit und für die Elementarladung setzen wir ein und erhalten:

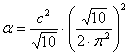(3‑27)

Durch Umformen erhält man:

(3‑28)

Und weil ist erhält man schließlich:

(3‑29)

Die Feinstrukturkonstante hängt somit statt von der Elementarladung nur von den Naturkonstanten c und ab und hat den dimensionslosen Wert von oder _.

Die absolute Abweichung zum CODATA-Wert beträgt nur 0,00000308104262349701 und relativ 0,0422213756059997 % bzw. .

Nach dem neuen Weltmodell wird die elektromagnetische Kraft (α) zwischen Elektronen und Protonen vom umgekehrtem Verhältnis der Planckmasse und der geometrischen Komponente verursacht.

(3‑30)

Mit der quantisierten Ladung können wir die Feinstrukturkonstante auch folgendermaßen formulieren:

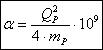(3‑31)

Mit der quantisierten Ladung und der Elektronenmasse erhalten wir die folgende Beziehung:

(3‑32)

Dieser Zusammenhang ist ziemlich ähnlich mit der hergeleiteten Formel (3-11) für den klassischen Elektronenradius aus dem letzten Abschnitt, wobei sich nur die Massen ändern:

Bei der obigen Formel (3-32) erkennt man auch die Ähnlichkeit der Feinstrukturkonstante mit der Gravitationskraft. Wir werden am Ende dieses Abschnitts die Gravitationskonstante herleiten und ein Vergleich der beiden Kräfte zeigt, daß die Feinstrukturkonstante eine Art "Gravitationskraft" in den Atomen beschreibt. Die Stärke der elektromagnetischen Kraft zwischen Protonen und Elektronen beruht nämlich wie die Gravitationskraft auf quantisierten Ladungen.