1.1. Die Herleitung der Erdbeschleunigung
Mit dem Kugelvolumen 
des klassischen Elektronenradius aus dem Abschnitt 3.3, das den Zusammenhang der Ladungsverteilung der Elementarladung in einem Kugelvolumen darstellt, können wir die Erdbeschleunigung als eine spezielle Dichtefunktion des Protons herleiten mit:
(3‑33)
Die Erdbeschleunigung ergibt sich als das Verhältsnis zwischen der Protonenmasse und der kugelförmigen Ladungsverteilung in einem Atom. Ausserdem enthält die Gleichung als Koeffizient den Zeitfaktor. Im Kapitel 4 werden wir das Phänomen mit dem Zeitfaktor im Abschnitt "Der Ursprung der Zeit" behandeln.
Die Erdbeschleunigung bzw. die Fallbeschleunigung ist von der Masse der fallenden Körper unabhängig, und deshalb fallen im Vakuum alle Körper gleich schnell. Jedoch ist die Fallbeschleunigung von der Dichte der anziehenden Körper abhängig. Auf jedem Himmelskörper gibt es deshalb unterschiedliche Fallbeschleunigungen, und die obige Herleitung bezieht sich auf die spezielle Dichte der anziehenden Körper.
Die obige Gleichung ist äquivalent mit:
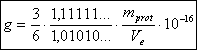(3‑34)
Und man kann sie auch folgendermaßen schreiben:
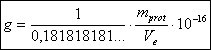(3‑35)
In gekürzter Form erhalten wir schließlich:
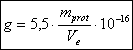(3‑36)
Der Zahlenwert für die Erdbeschleunigung beträgt mit 
und nach CODATA ist sie festgelegt mit 
.
Durch Umformung der obigen Gleichung kann man die Protonenmasse auch mit der Fallbeschleunigung berechnen mit:
(3‑37)
Hier erkennt man die direkte Abhängigkeit der Protonenmasse von der Fallbeschleunigung, die wir bei der Herleitung der Teilchenmassen besprochen haben.
