Der klassische Elektronenradius

Der "klassische Elektronenradius" ist aus der Analogie bei geladenen makroskopischen Hohlkugeln entstanden, und er beschreibt eine geladene Hohlkugel mit der Verteilung der Elementarladung auf der Kugeloberfläche. Aus dem Zusammenhang der Kapazität einer Kugeloberfläche und der Ruheenergie des Elektrons wurde der klassische Elektronenradius abgeleitet.

Dabei handelt es sich nicht um einen gewöhnlichen Radius eines Teilchens oder des Elektrons, sondern er beschreibt den Zusammenhang zwischen der Ladungsverteilung auf einer Kugeloberfläche und der Selbstenergie des Elektrons. Die Bezeichnung mit "Elektronenradius" ist irreführend, weil es sich nicht um den tatsächlichen Radius des "Teilchens" Elektron handelt.

Die Gleichung für den klassischen Elektronenradius lautet:

Da bei der Maxwellschen Formel mit gilt, erhalten wir für den klassischen Elektronenradius in gekürzter Form:

(3‑9)

und das entspricht genau dem folgenden Zusammenhang:

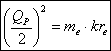(3‑10)

Der klassische Elektronenradius beschreibt somit das Verhältnis zwischen der Wechselwirkung der Elementarladung zur Masse des Elektrons.Wenn wir die Variablen mit ihren quantisierten Größen und ersetzen erhalten wir:

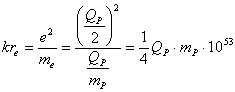(3‑11)

Damit können wir die Wechselwirkung der Ladungsverteilung auf einer Kugeloberfläche statt mit der Elektronenmasse auch mit der Planckmasse erklären.

Wir setzen in diese Formel die modifizierte Elementarladung aus dem Abschnitt 2.2 mit dem Wert und die im letztem Abschnitt hergeleitete Elektronenmasse mit ein und erhalten den klassischen Elektronenradius mit dem Wert:

(3‑12)

Oder mit und erhalten wir:

(3‑13)

Mit dem klassischen Elektronenradius und den quantisierten Größen können wir auch die Elementarladung berechnen:

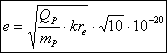(3‑14)

Berechnung des Protonenradius

In Atomen besteht ein direkter Zusammenhang zwischen der Ladungsverteilung der Elektronen und der Ladung der Protonen. Zur Überprüfung dieser Beziehung wurde deshalb der Protonenradius mit dem klassischen Elektronenradius hergeleitet.

Eine Raumkugel besitzt die Eigenschaften der Ladungsverteilung, die im klassischen Elektronenradius enthalten ist. Wir betrachten die beiden Radien und erhalten den Zusammen hang:

(3‑15)

Durch Umformung dieser Gleichung erhalten wir den Protonenradius mit:

(3‑16)

Durch Einsetzen von in die obige Gleichung erhalten wir den Zusammenhang zwischen dem Protonenradius und der quantisierten Ladung und Masse mit:

(3‑17)

Den Protonenradius können wir auch über den folgenden Zusammenhang mit den quantisierten Größen mit der Planckmasse und dem Planckvolumen berechnen:

(3‑18)

Das Verhältnis zwischen Masse und Volumen zeigt als Dichte allgemein den Anteil der Masse pro Volumeneinheit. Der Kehrwert der Dichte als spezifisches Volumen ist bei physikalischen Vorgängen auch von großer Bedeutung, wie wir später noch sehen werden.

Mit den o.g. Gleichungen bekommen wir für den modifizierten Protonenradius den Wert von . Nach Experimenten mit myonischem Wasserstoff am Paul Scherrer Institut beträgt der Radius des Protons und wir erhalten mit den hergeleiteten Gleichungen eine geringfügige Abweichung .

Für die Protonenmasse mit dem modifizierten Radius erhalten wir schliesslich einen Wert von . Auch aus den weiteren nun folgenden Zusammenhängen erhält man exakt diesen Wert für die Protonenmasse.

Die Berechnung der Protonenmasse

Mit dem klassischen Elektronenradius berechnen wir ein Kugelvolumen, das die Wechselwirkung der Elementarladung zur Elektronenmasse als Aufteilung in einem Kugelvolumen darstellt. D.h. statt der üblichen Hohlkugel betrachten wir eine ausgefüllte Kugel mit dem Volumen:

Mit dem Protonenradius berechnen wir auch ein Kugelvolumen, das die Bestandteile des Protons im Atomkern enthält:

Das Planckvolumen mit der halben Plancklänge als Radius erhalten wir mit:

Mit diesen Kugelvolumen erhalten wir für die Dichte des Protons im Atomkern den folgenden Zusammenhang mit den Planckgrößen:

(3‑19)

Die Dichte des Protons im Atomkern als das Verhältnis von seiner Masse zu seinem Volumen ist äquivalent mit dem Planckvolumen und dem Volumen nach dem klassischen Elektronenradius und dem Verhältnis zur Planckmasse . Zwischen der Protonendichte und der Raumverteilung der Planckmasse mit dem quantisierten Volumen besteht der Faktor 48.

Bildhaft kann man sich das folgendermaßen vorstellen: Das 48-fache Verhältnis des kleinsten Volumens mit der kleinsten Masse, die im Volumen des klassischen Elektronenradius enthalten ist, ergibt die Dichte des Protons. Die Dichte des Protons multipliziert mit der quantisierte Masse ergibt eine Kugel in der Größe des nach klassischem Elektronenradius mit 48 Planck-Kügelch en.

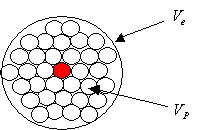
Abbildung:

Zusammenhang der Protonendichte und Planckvolumen

Die Protonenmasse können wir auch unabhängig von seinem Radius herleiten. Wir setzen in die Gleichung (Gl. 3-6) den Radius aus (Gl. 3-17) mit ein und erhalten die Masse des Protons mit den quantisierte Größen als:

(3‑20)

Dabei zeigt uns die umgestellte Gleichung mit

(3‑21)

dass die Protonenmasse in Anteilen der Planckmasse ein bestimmtes Planckvolumen ergibt.

Weil zwischen den Protonen und Elektronen ein enger Zusammenhang besteht und ihre Massen in einem bestimmten quantisierten Volumen enthalten ist, erhalten wir die folgende Beziehung:

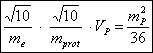(3‑22)

Die ersten beiden Terme sind für den Anteil der Planckmasse für das Elektron und Proton pro Raumkugel in dem Planckvolumen . Nach Umformung dieser Gleichung erhalten wir:

(3‑23)

D.h. die Masse des Protons und des Elektrons in Anteilen der Planckmasse ergibt das 360 fache Planckvolumen.

Wenn wir in die obige Gleichung statt die Massen des Elektrons und Protons die quantisierte Größen einsetzen erhalten wir mit und :

(3‑24)

Durch Umformung erhalten wir den Protonenradius mit:

(3‑25)

D.h. der Protonenradius ergibt sich aus einem bestimmten Verhältnis zwischen dem Plackvolumen und der Planckmasse.

Zusammenfassung der bisherigen Ergebnisse

Anhand der quantisierten Größen können wir mit den bisherigen Gleichungen den Protonenradius und die Masse des Protons und Elektrons herleiten und sie direkt über die neuen Planckeinheiten berechnen. Wir erhalten dabei bisher unbekannte Zusammenhänge, die in zukünftigen Projekten weiter analysiert werden.

Bei den hergeleiteten Gleichungen handelt es sich um fundamentale Zusammenhänge, weil sie auf quantisierten Größen basieren. Zum Beispiel ist der Zusammenhang bei der Elektronenmasse als das Verhältnis zwischen der quantisierten Ladung und der quantisierten Masse bereits in der kleinsten Dimension enthalten. Der Erweiterungsfaktor als Zehnerpotenz zwischen der kleinsten Dimension und der Dimension bei dem der Wert experimentell ermittelt wurde zeigt uns, daß sich dieser Zusa mmenhang erst ab bestimmten Größendimension bei unseren Messungen bemerkbar macht. Aber seine Bestandteile und die Zusammenhänge aus dem er besteht, existieren bereits in der kleinsten Dimension. Mit anderen Worten: Die experimentell gemessenen subatomaren Teilchen sind Ansammlungen von noch kleineren Teilchen, und ihre Eigenschaften basieren auf gleichen Zusammenhängen.

Der Zusammenhang zwischen Masse und Volumen, den wir als Dichte bezeichnen, existiert z.B. bei einem Apfel genauso wie bei der Erde, aber in verschiedenen Größendimensionen. Dieser fundamentale Zusammenhang der Dichte entsteht nicht erst wenn der Apfel eine bestimmte Größe erreicht hat, sondern der Apfel besteht an sich aus solchen Zusammenhängen.

Die minimalen Abweichungen in den mikroskopischen Größenskalen zwischen den gemessenen und den theoretischen Werten bei den Herleitungen beruhen neben technischen Meßungenauigkeiten auch auf den kleinsten Einflüssen der Gravitation bzw. der Fallbeschleunigung, die sich über mehrere Größenskalen aufsummieren.

Die gemessene Masse, oder genauer gesagt, das Gewicht eines Teilchens und somit auch des Protons hängt vom Ort ab. Auf der Erde sind die Fallbeschleunigung und die Gravitation nicht überall gleich. Wir würden auf der Erde abhängig von der geographischen Lage verschiedene Meßwerte für die Masse erhalten.

Deshalb muß man bei der Masse zwischen den empirischen Werten unter Gravitationseinwirkung und den tatsächlichen Werten unterscheiden. Man könnte zu den berechneten Werten die zusätzlichen Einflußfaktoren addieren, aber diese Einflußfaktoren, wie die Fallbeschleunigung, sind selbst vom Ort abhängig und deshalb auch variabel. Besser wäre es, bei Massenbestimmungen auch die ortsabhängige Fallbeschleunigung anzugeben. Im späteren Abschnitt werden wir de n direkten Zusammenhang zwischen der Protonenmasse und der Erdbeschleunigung besprechen.

Die Bausteine der Atome kann man mit dem neuen Weltmodell erklären, aber weil wir nur Massen und Radius analysiert haben, erhalten wir noch keine hinreichende Information über den Aufbau und die innere Struktur dieser Teilchen. Für ein neues Atommodell muß man alle anderen Eigenschaften der Atome auch berücksichtigen. Wenn man weitere experimentell gewonnenen Erkenntnisse über Atome auf die quantisierten Größen zurückführt, kann man auch ein besseres Bild von der inneren Struktur der Atome erhalten. In zukünftigen Projekten werden wir mit Hilfe der quantisierten Größen weitere Zusammenhänge analysieren und die innere Struktur der Atome mit den quantisierten Größen erklären.